Are There Uncreated Abstract Objects?

This is the weekly Q & A blog post by our Research Professor in Philosophy, Dr. William Lane Craig.

Question

First, as many others do, I'd like to thank you for your work as a philosopher, theologian, and Christian apologist. Your work has changed my life by revealing to me the intellectual side to a worldview that I, as a Christian, was becoming increasingly convinced was anti-intellectual. I regularly tell my friends that you are my favorite philosopher and Christian apologist, and it's chiefly because of your work that I want to study both philosophy and theology and become a Christian apologist. You'll always have my thanks.

I've been reading "Philosophical Foundations for a Christian Worldview" for the past few months and have repeatedly been fascinated by what I am reading. One of my favorite areas of philosophy is ontology, and I was particularly interested in abstract objects. I had heard you explain abstract objects briefly and often in your debates and lectures as one of the only two options for a first cause of the universe. As you've said, abstract objects do not stand in causal relations.

In thinking about this, however, something has come to mind. If abstract objects do not stand in causal relations, what is their relationship with God? Both God and abstract objects are metaphysically necessary beings, meaning that they exist in every possible world. This seems to me to conflict with a theological view that God is the creator of everything. If God didn't exist, nothing would. Though it seems to me that if God didn't exist, abstract objects still would. Thus, it seems that mathematical entities, for instance, would and do exist independently of whether or not God exists.

I am open to the idea that I'm totally wrong on this point, so here are my questions.

1. Do abstract objects exist independently of whether or not God exists?

2. If they do, then what is their relation to God, and does this have any theological implications (i.e. does this mean that God didn't create everything or that not everything is dependent on His existence)?

3. If they don't, then in what way are they dependent on God's existence?

Thank you for having a Q&A Section on your website. Even if my question isn't answered, I can always look forward to seeing something good in this section every Monday.

God bless.

Kevin

United States

Dr. William Lane Craig’s Response

Thanks for your encouraging words, Kevin! Your question, “What is the relationship of abstract objects with God?” is one that has preoccupied me for the last dozen years. I am convinced, as you are, that it is theologically unacceptable to hold, as some contemporary Christian philosophers do, that there exist beings which are uncreated by God. So we must reject Platonism, the view that there exist uncreated, abstract objects like numbers, properties, sets, and so forth.

Notice that the problem posed by Platonic objects is not just their necessary existence but more fundamentally their uncreatability. Even if abstract objects exist in every possible world, so that they exist necessarily, still one might hold that they are in every world causally dependent upon God for their being and so not, in one sense, “uncreated.” In that case, it is not true that were God not to exist, abstract objects would still exist. It is not so much their necessary existence, then, as their aseity, or self-existence, that undermines God’s status as the sole ultimate reality.

Now, taking mathematical objects as a case in point, we find a wide variety of both realist and anti-realist views on offer today, as the figure below illustrates:

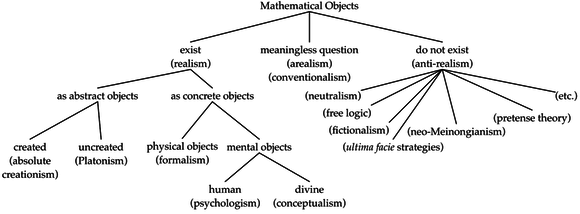
How one answers your several questions will depend on which view one adopts.

1. Do abstract objects exist independently of whether or not God exists? This is the view on our figure labeled Platonism, a form of realism which takes numbers, sets, and so on, to be abstract objects existing independently of God. You and I agree that this is not an option for the Christian theist. But all of the remaining views, whether realist or anti-realist, hold that abstract objects do not exist independently of God, either because they do not exist at all or because they exist dependently upon God.

2. If they do, then what is their relation to God, and does this have any theological implications? Only on the Platonist view do mathematical objects exist independently of God. This affirmation, besides being sub-biblical, has major theological implications.

As Brian Leftow has argued, God’s being the sole ultimate reality is a requirement of perfect being theology.[1] As a perfect being, the greatest conceivable being, God must be the self-existent source of all reality apart from Himself. For being the cause of existence of other things that exist is plausibly a great-making property, and the maximal degree of this property is to be the cause of everything else that exists. If mathematical objects existed independently of God, then God would be the source of merely an infinitesimal part of what exists. The physical universe which has been created by God is an infinitesimal triviality utterly dwarfed by the unspeakable quantity of uncreated beings.

Seen in this light, divine aseity is a corollary of God’s omnipotence, which belongs indisputably to maximal greatness. For if any being exists independently of God, then God lacks the power either to annihilate it or to create it. An omnipotent being can give and take existence as He sees fit with respect to other beings. God’s power would thus be attenuated by the existence of independently existing abstract objects.

Finally, there is a powerful argument against the existence of uncreated, Platonic properties. Consider the cluster of divine attributes which go to make up God’s nature. Call that nature Deity. On Platonism Deity is an abstract object existing independently of God to which God stands in the relation of exemplification or instantiation. Moreover, it is in virtue of standing in relation to this object that God is divine. He is God because He exemplifies Deity. Thus, on Platonism God does not really exist a se at all. For God depends upon this abstract object for His existence. Platonism does not simply postulate some object existing independently of God—a serious enough compromise of God’s sole ultimacy—but makes God dependent upon this object, thus denying divine aseity.

Worse, if possible: since aseity, like omnipotence, is one of the essential attributes of God included in Deity, it turns out that God does not exemplify Deity after all. Since aseity is essential to Deity, and God, on Platonism, does not exist a se, it turns out that God does not exist! On Platonism there may a demiurge, such as is featured in Plato’s Timaeus, but the God of classical theism does not exist. Theism is thus undone by Platonism.

3. If they don't, then in what way are they dependent on God's existence? The answer depends on which alternative you adopt.

Absolute Creationism is a sort of modified Platonism which holds that abstract objects exist but are dependent upon and so created by God, even if necessarily and eternally. The chief difficulty confronting Absolute Creationism is the so-called boot-strapping objection, which claims that in order to create, say, properties, God would already have to have properties, which is viciously circular. All of the remaining alternatives on our figure are non-Platonic views.

There are non-Platonic versions of realism which take mathematical objects really to be concrete objects, not abstract objects (Formalism, Psychologism, Conceptualism). The most discussed and most plausible of these non-Platonic realisms is Conceptualism, which takes mathematical objects to be thoughts in the mind of God, mental events of various sorts. This view has the advantage of being the historic, mainstream Christian position on so-called abstract objects and is the view I initially thought that I would defend when I began my study.

Arealism is a curious view which says that there just is no fact of the matter whether or not mathematical objects exist. It was the view of Logical Positivists of the 1930s, who denied that such metaphysical questions have any meaning. Whether we adopt talk of mathematical objects was taken to be just a matter of convenience; hence, the name Conventionalism. It seems to me that this is not an alternative open to Christian theists, since in every possible world God is the source of all reality other than Himself. Hence, there is a fact of the matter: uncreated mathematical objects do not and cannot exist.

That brings us to the cornucopia of anti-realist views of mathematical objects. According to these views abstract objects do not depend upon God for their existence, for abstract objects do not exist! These views have been largely overlooked by contemporary Christian philosophers. They merit greater consideration, since some of them seem to me to offer plausible and viable options to the Christian theist.

To give a quick rundown of the listed options:

Neutralism holds that reference to mathematical objects and even true existential statements about them do not imply their existence but are ontologically neutral.

Free Logic similarly holds that we can refer to things that do not exist, so that reference to mathematical objects is not ontologically committing.

Fictionalism holds that both existential statements about mathematical objects as well as statements referring to mathematical objects are simply not true.

What I call Ultima Facie Strategies (such Constructibilism, Modal Structuralism, and Figuralism) hold that mathematical statements need not be interpreted at face value (prima facie) but that there are alternative ways of understanding them (ultima facie interpretations) which do not commit us to the reality of mathematical objects.

Neo-Meinongianism, named for the early twentieth century Austrian philosopher Alexius Meinong, holds that there are things that do not exist (e.g., unicorns, centaurs, etc.) and that mathematical objects are among these.

Pretense theory, taking inspiration from work on make-believe and the nature of fiction, construes talk of mathematical objects as prescriptions to imagine something to be true, much in the way we imagine Sherlock Holmes to have lived at 221 B Baker St.

And that is not the end! There are still other anti-realist views to be considered.

So if you’re interested in pursing this fascinating question further, Kevin, I think you can see you’ve got your work cut out for you! To get started, I recommend my recent Cadbury Lectures “God over All” at the University of Birmingham, now available on DVD, and the fine six-views book edited by Paul Gould, Beyond the Control of God? Six Views on the Problem of God and Abstract Objects (London: Bloomsbury, 2014).